Abschlussprojekt

• Gruppenarbeit mit bis zu 2 Personen
• Versionsverwaltung mit git
• Umsetzen des Projektes, welches wir in diesen Einheiten besprechen werden
• Abgabetermin: 27.02.2025 um 23:55 Uhr

Umfang des Abschlussprojektes

• 35h pro Person * 2 Personen pro Gruppe = 70h pro Gruppe
• 35h pro Person setzt sich aus folgenden Annahmen zusammen:
  • gemeinsame LV: 60UE á 45min = 45h
  • Vor- & Nachbereitung inkl. 15 HÜ: 1,5h pro 2 UE = 45h
  • Kursumfang: 5 ECTS = 125h
  • 125h - 45h - 45h = 35h

Abschlussprojekt

• In den nächsten Folien wird ein Projekt inkl. minimaler Umsetzung/Anforderungen vorgestellt
• Diese minimale Umsetzung entspricht 60% der Gesamtpunkte
• Die restlichen 40% können durch Erweiterungen erreicht werden
• Von diesen max. 100% werden die Minuspunkte der Hausübungen abgezogen

Aufgabenstellung

• Eine Anwendung mit Web-UI (streamlit) soll entwickelt werden
• Die Umsetzung erfolgt in Python mit Objektorientierung
• In der Anwendung können beliebige ebene Mechanismen (mit gewissen Einschränkungen) definiert & deren Kinematik simuliert werden

Alternativen zu diesem Projekt werden zum Schluss diskutiert

Ebene Mechanismen

• Ebene Mechanismen (oft auch ebene Koppelgetriebe genannt) sind Mechanismen aus mehreren Gliedern die mit Dreh- und Schubgelenken verbunden sind
• Erzeugen Bewegungsabläufe in einer Ebenen → hängt von der Anzahl/Konfiguration der Gelenke & den kinematisch relevanten Abmessungen ab
• Ein Viergelenkgetriebe ist ein einfaches Beispiel für einen ebenen Mechanismus

Ebene Mechanismen

• Wir wollen nun solch einen ebenen Mechanismus simulieren
• In unserem Modell besteht ein Mechanismus aus Gelenken ("Punkten") und Gliedern ("Stangen")
• Wir wollen unseren Mechanismus immer für einen bestimmten/konstanten Drehwinkel betrachten

Einschränkungen

• Es werden nur ebene Mechanismen betrachtet
• Nur Drehgelenke verbunden mit starren Gliedern
• Nur Drehgelenk (1 rot. Freiheitsgrad) als Antrieb → ein Gelenk des Mechanismus bewegt sich auf einer Kreisbahn
• Ein Gelenk des Mechanismus ist statisch/fest verankert

Mathematische Modellierung

• Zur Simulation muss unser Mechanismus in ein mathematisches Modell überführt werden
• Im allgemeinen hat ein Punkt in der Ebene 2 Freiheitsgrade (- und -Koordinate) → unser Modell soll beschreiben wie diese Freiheitsgrade entzogen werden

Freiheitsgrade

• Anzahl der Gelenkspunkte
  • je 2 Freiheitsgrade pro Punkt für
  • → Freiheitsgrade im ganzen Mechanismus
• Anzahl der Glieder
  • verbinden je zwei Gelenkspunkte und → fixe Länge/fixer Abstand
  • → reduziert die Freiheitsgrade
• Randbedingungen (engl. boundary conditions)
  • reduzieren die Freiheitsgrade weiter
  • statische Randbedingungen → fixe Punkte
  • dynamische Randbedingungen → bewegte Punkte

Beispiel der Viergelenkkette

Beispiel der Viergelenkkette:

• Besteht aus Gelenken und 4 Gliedern → je 2 davon sind besonders und müssen speziell behandelt werden:
  • Gestell: Ist jenes Glied das fest ist → verbindet gedanklich mit → diese beiden Glieder sind statisch
  • Kurbel: Ist am Gestell angeschlossen und bewegt sich auf einer Kreisbahn → verbindet mit , es bleibt aber weiterhin statisch, und dynamisch → 1 Freiheitsgrad (Rotation)
  • Alle anderen Glieder: Verbinden zwei (dynamische) Punkte und halten deren Abstand konstant → und zu und zu

Beispiel der Viergelenkkette:

• Daraus folgt in unserer Art der Modellierung:
  • → , , (→ ist nur für die Kreisbahn notwendig)
  • → ist statisch
  • → ist auf einer Kreisbahn → bei konstantem wird vollständig bestimmt
  • bilden zusammen das Gestell & die Kurbel ab

Übrige Freiheitsgrade

• → "normale" Glieder notwendig
• Glieder zw. und sowie und berücksichtigen →
• →

Beispiel der Viergelenkkette:

• Wie kann über dieses Modell die Kinematik bestimmt werden?

Idee

• Die genaue Konfiguration des Mechanismus kann für einen konstanten Drehwinkel bestimmt werden
• wird nun variiert (z.B. in Schritte) → die Konfiguration des Mechanismus ändert sich mit einem Freiheitsgrad () → Kinematik des Systems

Wie kann die Konfiguration bestimmt werden?

• Wir können die Lage von allen Punkten bestimmen die mit Randbedingungen versehen sind
• Für diese neuen Lagen können die Längen der Glieder bestimmt werden → da sich die Punkte bewegt haben sind die Längen der Glieder nicht mehr korrekt
• Aus den aktuellen Ist-Längen und den Soll-Längen der Glieder kann ein Fehler bestimmt werden
• → Optimierung soll diesen Fehler minimieren

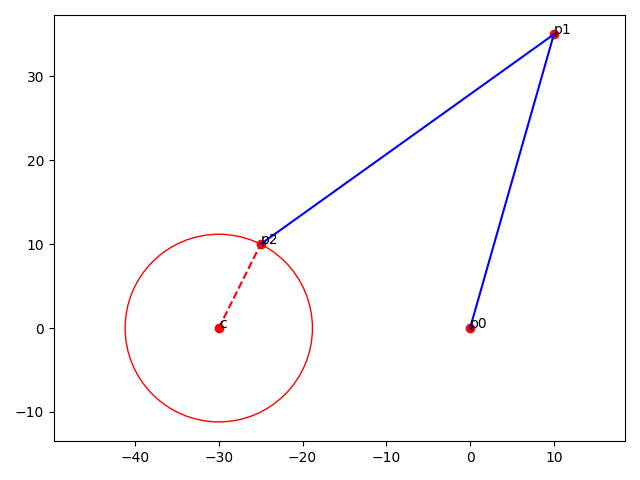
Viergelenk - Modell in Ausgangskonfiguration

• Wir sehen uns an wie dies mathematisch für das Viergelenk funktioniert
• Die Ausgangslage ist jene aus der Abbildung oben → in diese wird der Mechanismus modelliert:
  • → statisch BC → unbeweglich
  • → dynamisch BC → Kreisbewegung um
  • → Mittelpunkt der Kreisbahn
• Der Drehwinkel wird als initialisiert

Viergelenk - Bestimmen der Längen

• Für jeden Schritt der Berechnung wird (temporär) konstant gehalten
• Der Vektor beinhaltet alle Punkte des Systems:

• Aus den Gliedern des Systems lässt sich die Matrix ableiten, die nur die Elemente , und enthält und damit die Verbindungen der Punkte (= Glieder) beschreibt:

• Das Produkt ergibt den Vektor der Längen der Glieder für den aktuellen, konstanten Winkel enthält
• Diese sind in komponentenweise angeordnet

Viergelenk - Bestimmen der Längen

• Um aus die tatsächlichen Längen der Glieder zu erhalten, wird umgeformt in und über die zeilenweise angewendete euklidische Norm der Vektor berechnet:

• enthält nun die Längen aller Glieder:

Viergelenk - Bestimmen der Längen

• mit den konkreten Zahlen der Anfangskonfiguration ergibt sich:

Viergelenk - Matrizen

• Wird nun um erhöht, so ändert sich die Konfiguration des Mechanismus
• Aufgrund der Kreisbewegung von ändert sich dessen Position zu , alle anderen Punkte bleiben unverändert

Viergelenk - Matrizen

• nun können die beiden Längenvektoren und verglichen werden
• der Fehler ergibt sich aus der Differenz der beiden Vektoren:

• dieser Fehler kann nun im Sinne der kleinsten Fehlerquadrate minimiert werden → z.B. mit Funktionen aus dem scipy.optimize-Modul

Minimalanforderungen

• Softwareprojekt in Python mit Objektorientierung
• Versionskontrolle über git & GitHub
• Anwendung mit Web-UI:
  • Simulation von Mechanismen und deren Kinematik (Detail siehe unten)
• Software-Dokumentation:
  • requirements.txt-Datei mit allen packages
  • README.md im Repository mit Anleitung zur Installation und Ausführung
• Projekt-Dokumentation - Zwei Möglichkeiten
  • README.md ergänzen um umgesetzten Erweiterungen, UML-Diagrammen der Softwarestruktur, Quellen zu verwendeten Inhalten etc.
  • ODER
  • Kurzer Bericht als pdf-Dokument mit selbem Inhalt

Minimalanforderungen 1/2

• Eine Python-Anwendung mit Web-UI (streamlit) soll entwickelt werden
• Darin können beliebige ebene Mechanismen mit unseren Einschränkungen definiert werden
• Die Positions-Kinematik des Mechanismus soll für den Winkel im Bereich von bis berechnet werden
• Der Mechanismus und seine Kinematik bzw. die Bahnkurven der Punkte werden visualisiert
• Die Bahnkurve kann als -Koordinaten im csv-Format (o.ä) abgespeichert werden
• Der Mechanismus selbst (und damit seine Kinematik) soll gespeichert und geladen werden können
• Die Kinematik soll als Optimierungsproblem gelöst werden, bei der die Länge-Fehler der Glieder minimiert werden → siehe Erklärung oben

Minimalanforderungen 2/2

• Es muss verifiziert werden, dass der Mechanismus valide ist
• Testen der Implementierung am Beispiel des "Strandbeest" bzw. an einem seiner Beine → in Dokumentation zeigen
• Die Anwendung soll mit streamlit deployed werden

Mögliche Erweiterungen

• Visualisierung der Längen-Fehler aller Glieder als Funktionen des Winkels
• Animation als Video/gif speichern
• Overlay z.B. von Winkeln oder Längen auf die Visualisierung
• Lösen von Kinematiken ermöglichen bei denen ein Punkt noch einen Freiheitsgrad hat → z.B. eine Schubkurbel
• Definition einer Auszeichnungssprache um Modelle der Mechanismen zu beschreiben → Modell kann heruntergeladen und ggf. hochgeladen werden
• Optimieren der Gliederlängen für eine bestimmte Bahnkurve bzw. einer Bahnkurve die gewissen Kriterien entspricht

Mögliche Erweiterungen

• Alternative Ansätze im UI z.B. Drag and Drop oder Sketches
• Import von Sketches mit Bildererkennung (kariertes Papier, etc.)
• Erstellen einer Stückliste für ausgewählte Gestänge, Antriebe und Gelenke
• Berechnung der maximalen Vorwärts-Geschwindigkeit (z.B. eines festgelegten Punktes in X) eines Strandbeests in Abhängigkeit von der Drehgeschwindigkeit der Kurbel, Schrittlänge und maximale Schritthöhe → das könne eine Metrik für die Optimierung der Gliederlängen sein
• 3D-Volumenmodell des Mechanismus mittels OpenSCAD erstellen
• Sehr große Erweiterung: Kräfte/Momente berücksichtigen (Kinetik) und dadurch die Positions-, Geschwindigkeits- und Beschleunigungskinematik bestimmen

Abgabe

• Abgabetermin: 27.02.2025 um 23:55 Uhr
• Alle Gruppenmitglieder müssen den Link zum Repository auf Sakai abgeben
• Der Beitrag der einzelnen Mitglieder wird anhand ihrer Commits beurteilt → jedes Mitglied soll aktiv und inhaltvoll am Projekt mitarbeiten
• Es wird der letzte Commit im main bzw. master-Branch bewertet

Alternatives Abschlussprojekt

• Falls die Aufgabenstellung einer Gruppe nicht zusagt, kann ein alternatives Abschlussprojekt mit dem jeweiligen Vortragenden vereinbart werden
• In der ersten Hälfte des letzten Termins der LV muss diese Aufgabenstellung mit dem Vortragenden vereinbart werden → anschließend wird sie mit dem Vortragenden der anderen Gruppe abgestimmt

Was muss vereinbart werden?

• Idee des eigenen Projektes
• Minimalanforderungen → Programmiersprache, Versionsverwaltung, Dokumentation, etc. bleibt immer gleich
• Mögliche Erweiterungen
• Diese sind dann verbindlich für die jeweilige Gruppe → es kann aber immer auf das allgemeine Projekt zurück gewechselt werden