Beispiel: Darstellung von strukturierten Dokumenten

• Wir wollen Dokumente mit Struktur (Überschriften, Absätzen, Bildern, etc.) speichern, übertragen & darstellen
• Welche Eigenschaften muss die Datenstruktur haben?
  • Flexibel erweiterbar
  • Verschachtelte Elemente möglich
  • einfach im Handling
• Für das Web wird hierfür das Document Object Model (DOM) genutzt → die Struktur hinter einer HTML-Datei

Bäume & Graphen

• Alle Datenstrukturen die wir bis jetzt betrachtet haben waren linear bzw. Mischformen wie die Hash-Tabelle

• Viele Daten die wir in der Realität haben lassen sich aber nur schlecht in sequentielle Form packen

Bäume

Beispiel - Taxonomie von Datenstrukturen

• Beispielsweise auch diese Taxonomie von Datenstrukturen lässt sich nicht sequentiell abbilden

Bäume

• Bäume sind Datenstrukturen die uns bereits in einigen Beispielen (unbewusst) begegnet sind
• Sie bilden hierarchische Strukturen ab → sinnvoll für kombinatorische Probleme

Aufbau eines Baumes

• Knoten die über Kanten miteinander verbunden sind → ähnlich einer Liste
• Es gibt genau eine Verbindung zw. 2 Knoten → einer der Knoten ist der Elternknoten, der andere der Kindknoten
• Es gibt genau einen Knoten ohne Eltern → Wurzel
• Es kann beliebig viele Knoten ohne Kinder geben → Blätter
• Üblicherweise wird die Wurzel ganz oben dargestellt und darunter die Kinder bzw. weitere Nachkommen

Bäume

Bäume

• Durch Start beim Wurzelknoten kann man sich entlang der Kanten zu jedem beliebigen Knoten "durchhangeln" → ein Pfad
• Jede Abzweigung entspricht z.B. einer Frage oder Entscheidung:
  → "Ist die Datenstruktur linear oder nicht-linear?"
  → "Ist die Datenstruktur statisch oder dynamisch?"

• Die Antwort liefert den nächsten Schritt
• Der Pfad identifiziert dadurch jeden Knoten genau
• → wird so z.B. im Machine Learning genutzt

Bäume

Arten/Eigenschaften von Bäumen

• Binärbaum:
  • jeder Knoten hat genau zwei Kinder
• Suchbaum:
  • ein Baum bei dem die Elemente im Baum sortiert eingeordnet werden → wenn der Baum balanciert ist
• Können kombiniert werden → Binärer Suchbaum
• Weiters:
  • AVL-Baum, Rot-Schwarz-Baum, etc.
  • MinHeap, MaxHeap als verwandte Datenstrukturen

Beispiel - tree_example.ipynb

• Erstellen aller notwendigen Klassen
• Traversieren durch den Baum
• Parsen einer HTML-Datei

Traversieren durch Bäume - Breitensuche

Bildquelle: https://commons.wikimedia.org/wiki/File:Breadth-First-Search-Algorithm.gif

Traversieren durch Bäume - Tiefensuche

Bildquelle: https://commons.wikimedia.org/wiki/File:Depth-First-Search.gif

Binärer Suchbaum

• Wir können einen binären Suchbaum nutzen um Elemente zu sortieren → beim Einfügen wird vorgegangen wie bei einer Binärsuche
• Wir können damit auch ein assoziatives Array implementieren

Beispiel - bs_tree_example.ipynb

• Erstellen eines binären Suchbaums
• Automatisches sortieren der Elemente
• Implementieren der __contains__(...)-Methode um den Baum zu durchsuchen

Aufgabe

• Wir wollen wieder mathematische Ausdrücke lösen, bzw. in eine lösbare Form bringen
  • In einer Hausübung bereits mit dem Dijkstra-Two-Stack-Algorithmus gelöst
  • Nun wollen wir einen Binärbaum nutzen
• Dieses Konzept wird auch in vielen anderen Fällen genutzt
  • Analyse von Texten (z.B. im natural language processing)
  • um Quellcode automatisch zu interpretieren
• Ausgangslage stellt die Datei parse_tree_start.py dar

Aufgabe

• Es gelten folgende Regeln für das aktuelle Zeichen c:
  1. c == '(': füge einen neuen Knoten als linkes Kind des aktuellen Knotens ein und gehe zum linken Kind
  2. c ein Operator (+, -, *, /): setze den Wert des aktuellen Knotens auf den Operator und füge einen neuen Knoten als rechtes Kind des aktuellen Knotens ein und gehe zum rechten Kind
  3. c eine Zahl: setze den Wert des aktuellen Knotens auf die Zahl und gehe zum Elternknoten
  4. c == ')': gehe zum Elternknoten

Aufgabe

Lösung - Dijkstra-Two-Stack-Algorithmus mit Baum

Musterlösung - parse_tree.py

• Klassendefiniton für Knoten eines Binärbaums, mit insert_left(...), insert_right(...) anstelle von Selbstordnung
• Algorithmus um Baum-Objekt aufzubauen
• Funktion um den ursprünglichen Ausdruck wieder aus dem Baum zu rekonstruieren

Binärer Suchbaum

• Für alle Operationen im Mittel effizient
• Es wird in jedem Fall eine Binärsuche angewendet um das zu behandelnde Element zu finden
• Worst-case Performance tritt ein, wenn der Baum nicht mehr balanciert ist → selbst-balancierende Bäume

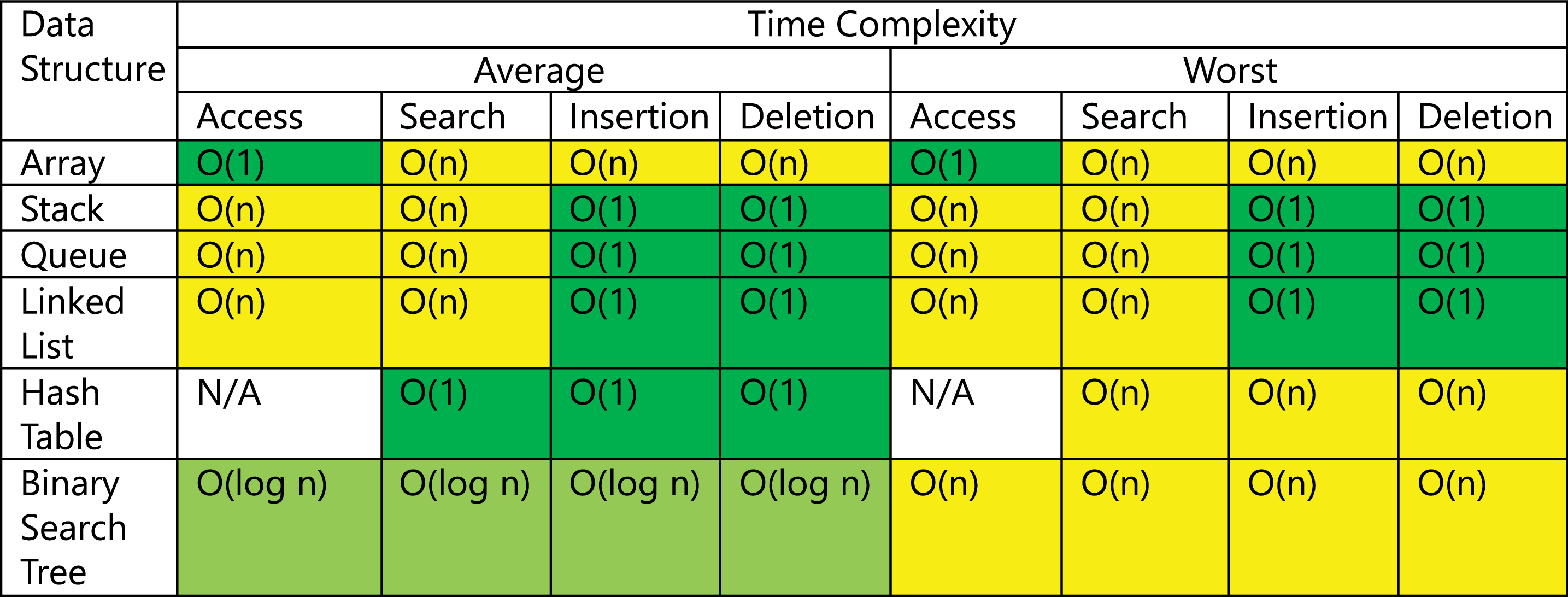
Bildquelle: [Althoff 2021]

AVL-Bäume (nach Georgi Maximowitsch Adelson-Welski und Jewgeni Michailowitsch Landis)

• Sind eine gängige Variante von selbst-balancierenden Bäumen → Performance degradiert nicht mehr
• Es wird ein Balancefaktor eingeführt der den Höhenunterschied der beiden Sub-Bäume eines Knoten darstellt
• Knoten können so eingefügt werden, dass der Baum balanciert bleibt
• Sollte eine Höhenkorrektur notwendig sein kann dies durch eine sogenannte Rotation erreicht werden

Heaps

• Datenstruktur in der ein Paar an Daten gespeichert wird
  • Wert (Daten)
  • Priorität (z.B. Position im Baum beim horizontalen Traversieren)
• Wird üblicherweise mit einem Baum implementiert → Art des Heap hängt vom verwendeten Baum ab
• Gängige Arten an binären Heaps:
  • Max-Heap: Elternknoten hat immer höhere Priorität als Kinder
  • Min-Heap: Elternknoten hat immer niedrigere (oder gleiche) Priorität als Kinder

Anwendung - Vorrangwarteschlange

• Wenn ein neues Element eingefügt wird, wird es nach Priorität gereiht
• Implementierung mit Heap erlaubt Operationen in

Heaps

• Kann effizient mit einer Liste abgebildet werden, die auf anhand einer Baumstruktur sortiert wird
  • Wurzel: Index 0
  • Knoten k: Index k
    • Linkes Kind von k: Index 2*k + 1
    • Rechtes Kind von k: Index 2*k + 2

Beispiel mit heapq-Modul - priority_queue_heap.py

from heapq import heapify, heappop, heappush

passenger_list = []
heappush(passenger_list, (3, "Daniel"))
heappush(passenger_list, (2, "Klaus"))
heappush(passenger_list, (1, "Markus"))
heappush(passenger_list, (2, "Thomas"))
heappush(passenger_list, (1, "Andreas"))

while passenger_list:
  print(heappop(passenger_list))

# (1, 'Andreas')
# (1, 'Markus')
# (2, 'Klaus')
# (2, 'Thomas')
# (3, 'Daniel')

Graphen

Beispiel: Routenplanung bei begrenzter Reichweite

• Wir möchten eine Routenplanung für Elektrofahrzeuge implementieren
• Das Fahrzeug soll sich mit seiner begrenzten Reichweite von Ladestation zu Ladestation bewegen können
• Welcher Weg soll gesucht werden?
  • Kürzester Weg
  • Schnellster Weg
  • Wenigste Ladestopps, etc.
    

Graphen

• Sind eine Verallgemeinerung des Konzeptes eines Baums
• Eigenen sich um viele Problemstellungen zu beschreiben
  • Straßennetze
  • Elektrische Schaltungen bestehend aus Mehrpolen
  • Netzwerk an Personen auf LinkedIn

Aufbau eines Graphen

• Knoten die mit Kanten verbunden sind
• Ein Knoten kann mit beliebig vielen anderen Knoten verbunden sein → es gibt keine Hierarchie zwischen den Knoten mehr
• Eine Kante kann ungerichtet oder gerichtet (Durchlaufen nur in diese Richtung möglich) sein
• Eine Kante kann gewichtet sein → gibt die Kosten beim Durchlaufen an

Graphen

• Der ADT eines Graphen kann (wie immer) auf diverse Arten implementiert werden
• In Python bietet sich ein Dictionary an
  • Schlüssel: Knoten
  • Wert: Dictionary mit allen Knoten die mit dem Schlüssel verbunden sind
    • Schlüssel: Knoten
    • Wert: Gewicht der Kante

Beispiel

# node: {node: weight, node: weight}
graph = {
  "n1": { "n2": 1, "n3": 5 },
  "n2": { "n1": 1, "n3": 7 },
  "n3": { "n1": 5, "n2": 7, "n4": 8 },
  "n4": { "n3": 8 }
}

Pfadsuche in Graphen

• Wir wollen den kürzesten (gewichteten) Pfad zwischen zwei Knoten finden → Gewicht entspricht z.B. Distanz, Zeit, etc.
• Wie bei Bäumen haben wir hier zwei Varianten
  • Breitensuche
  • Tiefensuche
• Pfad von n2 nach n4: n2 → n1 → n3 → n4 wenn Gewichte berücksichtigt werden

Dijkstra's Algorithm

• Modifikation der Breitensuche → Greedy-Algorithmus
• Wir starten bei einem Knoten und fügen alle über eine Kante erreichbare Knoten zu einer Warteschlange hinzu

Pseudocode

Algorithm Dijkstra(G, s):

Input: A graph G and a start node s that is part of G
Output: List of shortest paths from s to all other nodes in G

  D = map of distances from s to all other nodes in G initialized to ∞
  D[s] = 0
  Q = empty queue
  Q.enqueue(s)

  while Q is not empty:
    u = Q.dequeue()

    for each node v adjacent to node u:
      possible_route = D[u] + v.weight
      if possible_route < D[v]:
        D[v] = possible_route
        Q.enqueue(v)
  return D

Aufgabe

• Wir wollen nun diese einfache Variante des Dijkstra-Algorithmus implementieren
• Wir beschränken uns auf ungerichtete Graphen und die einfachste
• Dazu betrachten wir wieder folgenden Graphen:

  graph = {
    "n1": { "n2": 1, "n3": 5 },
    "n2": { "n1": 1, "n3": 7 },
    "n3": { "n1": 5, "n2": 7, "n4": 8 },
    "n4": { "n3": 8 }
  }
  

Dijkstra's Algorithm

• Hier enthalten sind 3 mögliche Implementierungen des Algorithmus

Musterlösung - dijsktra_algorithm.py

• Wir werden uns 3 mögliche Implementierungen ansehen
  • Mit einer simplen Warteschlange
  • Mit einer Vorrangwarteschlange die auf einem Heap basiert
  • Mit einer Vorrangwarteschlange und einer Liste um den Pfade zu rekonstruieren
• Die letzte ist jene die tatsächlich in der Praxis verwendet wird

Implementierung mit networkx-Modul

• Wir werden selten Graphen und dazugehörige Algorithmen vollständig selbst definieren
• Bibliotheken wie networkx bieten eine Vielzahl an Funktionen → u.a. eine (recht) effiziente Implementierung von Dijkstra's Algorithmus

Beispiel - networkx_example.py

import networkx as nx

graph = nx.Graph()
for i in range(1, 4+1):
    graph.add_node(f"n{i}")

graph.add_edge("n1", "n2", weight=1)
graph.add_edge("n1", "n3", weight=5)
graph.add_edge("n2", "n3", weight=7)
graph.add_edge("n3", "n4", weight=8)

path_with_weight = nx.shortest_path(graph, "n2", "n4", weight="weight")
print(path_with_weight)

# ['n2', 'n1', 'n3', 'n4']

Hausübung

• Wir wollen für eine fiktive Logistikfirma bestimmen welche Reichweite eine Flotte an Elektro- oder Wasserstofffahrzeugen haben muss um Lieferungen in ganz Europa durchführen zu können
• Hierzu haben wir einen DataFrame mit Städten und deren Koordinaten
• Wir wollen nun einen Graphen erstellen der die Verbindungen zwischen den Städten darstellt und die Reichweite der Fahrzeuge berücksichtigt