Beispiel: Wahl der Jahrgangsvertretung

• Wir möchten die Jahrgangsvertretung wählen, der Wahlsieger kann nur durch eine absolute Mehrheit bestimmt werden
• Es gibt 42 mögliche Wählende und 3 Kandidaten, es haben 38 Personen von ihrem Wahlrecht Gebrauch gemacht
• Die abgegebenen Stimmen sind in folgender Liste zusammengefasst:

  votes = ['Matthias', 'Julian', 'Franz', 'Julian', 'Julian', 'Matthias', 'Julian',
   'Franz', 'Julian', 'Matthias', 'Matthias', 'Franz', 'Matthias', 'Julian',
   'Franz', 'Franz', 'Matthias', 'Franz', 'Franz', 'Franz', 'Matthias', 'Franz',
   'Julian', 'Franz', 'Matthias', 'Franz', 'Julian', 'Julian', 'Julian',
   'Julian', 'Franz', 'Julian', 'Julian', 'Matthias', 'Franz',
   'Franz', 'Franz', 'Matthias']   
  

• Wir können nun durch die Liste iterieren und z.B. jede Stimme mit allen anderen vergleichen
• Ist dieser Ansatz noch gangbar wenn bei der österreichischen Nationalratswahl 4.929.745 Stimmen für 12 Parteien abgegeben wurden?

Analyse von Algorithmen

• Algorithmus liefert für definierten Input in endlicher Anzahl an Schritten einen definierten Output
• Es gibt viele mögliche Implementierungen für einen allgemeinen Algorithmus vgl. Lösung des Rucksackproblems
• Es müssen also Bewertungskriterien definiert werden

Bewertungskriterien

• Geschwindigkeit
• Speicherbedarf
• Komplexität in Implementierung & Wartung
• Erweiterbarkeit
• etc.

Geschwindigkeit → Zeitkomplexität

• Simpler Ansatz: Wir messen die Laufzeit die unser Algorithmus braucht
• Dieser empirische Ansatz ist abhängig von z.B. der Hardware, der Programmiersprache, der genauen Implementierung, der aktuellen Systemauslastung, etc.

Beispiel - simple_benchmark.py

• perf_counter() aus dem time Modul liefert relativen Zeitstempel mit der höchsten verfügbaren Auflösung

  import time
  start_time = time.perf_counter()
  
  # Algorithmus
  sum = 0
  for i in range(0, 10000):
    sum += i**2
  
  end_time = time.perf_counter()
  total_time = end_time - start_time
  print(F"Took {(total_time*1e3):.4f} milliseconds")
  
  #Took 1.7423 milliseconds
  #Took 1.5552 milliseconds
  #Took 1.6228 milliseconds
  #Took 1.5278 milliseconds
  

Zeitkomplexität

• Vergleich so nur sinnvoll wenn wir die selbe Hardware, Programmiersprache, Systemauslastung, etc. garantieren können

Alternativer Ansatz:

• Robustere Idee: Wir zählen die Anzahl der Operationen die unser Algorithmus ausführt

• Wir definieren eine Funktion die die Anzahl der Operationen in Abhängigkeit der Eingabegröße angibt

• Operationen in simple_benchmark.py:

  • Initialisierung von sum = 0
  • Quadrieren von i in jedem Schleifendurchlauf ( mal)
  • Addition von i**2 zu sum in jedem Schleifendurchlauf ( mal)
  • für Schleifendurchläufe

Aufgabe

• Bestimmen Sie die Anzahl an Operationen für folgende Funktion aus contains_duplicates.py
• Was wird hier sinnvollerweise mit bezeichnet?

  def contains_duplicates(array):
    for i, outer in enumerate(array):
      for j, inner in enumerate(array):
        if i != j and outer == inner:
          return True
    return False
  
  array = [0, 2, 5, 8, 3, 5, 3, 1, 7, 9]
  has_dupes = contains_duplicates(array)
  # has_dupes = True
  

Zeitkomplexität

• Offene Fragen in der Definition von :
  • Wie definieren wir ?
  • Welche Operationen zählen wir, z.B. wenn if-Anweisungen vorkommen
• Exakte Bestimmung von ist oft nicht möglich

neuer Ansatz:

• Verhalten für große ist entscheidend → exakte Bestimmung von nicht erforderlich!
• Nur mehr Programmteile mit dominierender Komplexität werden gezählt: z.B.: →
• Wird ausgedrückt mit (Landau-Symbol od. Big-O-Notation)
• Math. präziser:
  • gibt asymptotische obere Schranke für an
  • → wächst höchstens so schnell wie

Zeitkomplexität

• Hieraus ergeben sich bestimmte Komplexitätsklassen die üblicherweise angegeben werden

Übliche Komplexitätsklassen:

• : konstante Laufzeit
• : logarithmische Laufzeit *
• : lineare Laufzeit
• : linearithmische Laufzeit *
• : quadratische Laufzeit
• : polynomielle Laufzeit
• : exponentielle Laufzeit

* Im Allgemeinen wird hier mit der Logarithmus zur Basis 2 gemeint →

Übliche Komplexitätsklassen

• Primitive Operationen:

  i = i + 1          # O(1)
  j = 10 * i         # O(1)
  

• Schleifen über n: Komplexität des Schleifenkörpers mal Anzahl der Schleifendurchläufe

  i = 0
  while i < 10:
    i = i + 1        # O(1)
                     # = O(n * 1) = O(n)
  

• Sequenzen von Operationen: Summe (= Maximum) der Komplexität der Sequenz

  i = 0              # O(1)
  while i < 10:
    #do something... # O(...)
    i = i + 1        # O(n)
  j = 10 * i         # O(1)
                     # = O(n) + O(1) + O(...)
  

• Schleifen mit exponentiellem Inkrement

  i = 1
  while i < 10:
    i = i * 2        # O(1)
                     # = O(log(n)), da Inkrement exponentiell
  

Übliche Komplexitätsklassen

• In der Praxis sind die meisten Algorithmen in , oder

Aufgabe

• Bestimmen Sie die Komplexität für folgende Funktion aus element_in_list.py

  def element_in_list(array, element):
    for array_elem in array:
      if array_elem == element:
        return True
    return False
  
  array = [0, 2, 5, 8, 3, 4, 6, 1, 7, 9]
  has_element = element_in_list(array, 4)
  # has_element = True
  

Übliche Komplexitätsklassen

• Vielfach wird noch in die Fälle best-case, average-case und worst-case unterschieden
• Ausgangslage für Analyse faktisch immer der worst-case

Beispiel: Lineare Suche in einem Array

• Best-case:
  • Gesuchtes Element an Index 0 →
• Average-case:
  • Im Durchschnitt ist das gesuchte Element in der Mitte der Liste →
• Worst-case:
  • Gesuchtes Element nicht in der Liste →

Zeitkomplexität von Datenstrukturen

• In Algorithmen arbeiten wir für gewöhnlich mit den uns bekannten Datenstrukturen
• Für deren gängige Operationen kann eine Zeitkomplexität angegeben werden
• Kommt auch wieder auf die genaue Implementierung des abstrakten Datentyps an

Beispiele

• list.insert(0, x) fügt ein Element x am Anfang einer Liste ein

• Die Länge der Liste hat keine Auswirkung auf die Operation:

• np.insert(arr, i, x) fügt x an der Position i in ein Array ein

• Die Länge des Arrays hat einen Einfluss auf die Operation:

Zeitkomplexität von Datenstrukturen

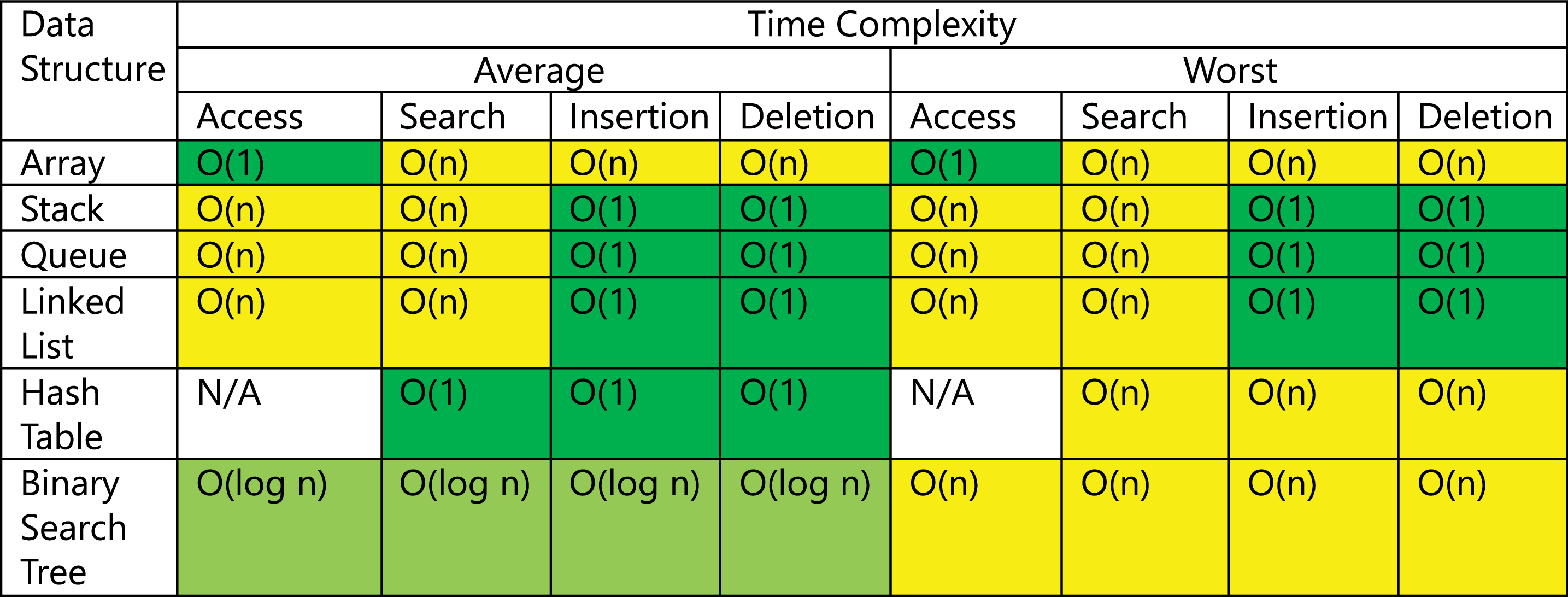
Bildquelle: [Althoff 2021]

Zeitkomplexität

• Praktische Bedeutung von Zeitkomplexität an einem gängigen Algorithmus der Mechatronik

Beispiel DFT vs FFT: time_complexity_dft.ipynb

• DFT - Discrete Fourier Transform:
• FFT - Fast Fourier Transform:

Auswirkungen

• Schon bei ist die FFT um den Faktor schneller als die DFT
• Bei einer Samplerate von entspricht einer verarbeiteten Datenmenge von
• Echtzeitanwendungen faktisch nur mit FFT möglich

Video on FFT

Platzkomplexität

Platzkomplexität

• Analog zur Zeitkomplexität kann auch die Platzkomplexität angegeben werden
• Speicherbedarf (RAM) wird analysiert
• Großer Unterschied: Platz kann wiederverwendet werden, Zeit nicht

Teilbereiche

• Fixer Speicher: für Algorithmus selbst
• Variabler Speicher: für Eingabedaten
• Speicher für temporäre Variablen: für Zwischenergebnisse während der Ausführung

Beispiel:

x = 1                     # O(1)
n = 5                     # O(1)
for i in range(1, n + 1): # range is like a generator (saves memory)
  x = x * i               # O(1), da x immer wieder überschrieben
                          # = O(1)

Platzkomplexität

Beispiel time_and_space_complexity_factorial.py

def factorial_iterative(n):
  """Iterative implementation of the factorial function with O(1)."""
  result = 1
  for i in range(1, n + 1):
    result *= i
  return result

def factorial_recursive(n):
  """Recursive implementation of the factorial function with O(n)."""
  if n == 0:
    return 1
  else:
    return n * factorial_recursive(n - 1)

Hausübung

• Definieren und Implementieren eines Algorithmus um zu bestimmen ob in ein Kandidat einer Wahl die absolute Mehrheit hat.