Scientific Computing I

Lernziele

• Studierenden können Daten mit numpy auswerten
  • Zeitreihen
  • Matrizenmultiplikation
  • etc.
• Studierende können Daten mit matplotlib visualisieren

Motivation - Rotationsmatrix

Motivation - Rotationsmatrix

• um die aktuelle Position des Werkzeugs im Raum zu ermitteln, muss die Steuerung des Roboters ständig Matrixmultiplikationen durchführen
• wenn dies nicht schnell genug möglich ist, dann kann der Roboter nicht mehr präzise arbeiten

Drehung durch Matrixmultiplikation

Motivation - Rotationsmatrix

• Matrixmultiplikationen sind in der Regel sehr rechenintensiv
• Dies soll am Beispiel des Skalarproduktes verdeutlicht werden

Skalarprodukt als einfachste Matrixmultiplikation

• Benötigt Multiplikationen und Additionen

Aufgabe

• Schreiben Sie ein Skript, das alle Zahlen zweier gleich langer Listen elementweise multipliziert und die Ergebnisse auf-addiert (entsprechend einer Matrixmultiplikation)

Ausgangslage - matmul_start.py

import random
import time

#Set a random seed
random.seed(42)

# Define the range for random numbers
min_value = 1  # Minimum value
max_value = 100  # Maximum value

# Generate the two lists of 10_000_000 random numbers each
list1 = [random.randint(min_value, max_value) for _ in range(10000000)]
list2 = [random.randint(min_value, max_value) for _ in range(10000000)]

start_time = time.perf_counter()
# Continue here:

Lösung - Python native

• Timing mit time.perf_counter()
• zip() um zwei Listen gleichzeitig zu durchlaufen

Musterlösung - matmul_solution_native.py

# Start the timer
start_time = time.perf_counter()

result = 0

for first_number, second_number in zip(list1, list2):
    multiplication_result = first_number * second_number
    result = result + multiplication_result

print("--- %s seconds ---" % (time.perf_counter() - start_time))
print(result)

• Resultat: ca. 0.7 Sekunden (früher ca. 2.8 Sekunden)

Lösung - Numpy

• Import des Pakets numpy → normalerweise mit Alias np
• Umwandeln der Listen in numpy Arrays
• np.matmul() bzw. @ für die Matrixmultiplikation

Musterlösung - matmul_solution_numpy.py

# Paket für numerische Aufgaben im Python
import numpy as np

# Umwandlung der Listen in numpy arrays
# vgl. Konstruktor
array1 = np.array(list1, dtype=np.int64)
array2 = np.array(list2, dtype=np.int64)

# %%
start_time = time.perf_counter()

# Aufruf der Funktion für Matrixmultiplikation des Pakets numpy
result = np.matmul(array1, array2)
print("--- %s seconds ---" % (time.perf_counter() - start_time))
print(result)

• Resultat: ca. 0.0166 Sekunden → ca. 40-fach schneller

Lösung - C

• Ergebniss lässt sich auch mit C-Implementierung vergleichen
• Üblicherweise noch schneller als numpy
• Mit Compiler-Flag -O3 optimieren

Musterlösung - matmul_solution_c.c

int main(){
    int amt = 10000000;
    
    int* list1 = malloc(sizeof(int) * amt);
    int* list2 = malloc(sizeof(int) * amt);
    if(list1 == NULL) { printf("Not enough memory!"); return -1; }
    if(list2 == NULL) { printf("Not enough memory!"); return -1; }
    
    for(int i = 0; i < amt; i++){
        list1[i] = (rand() % 100) + 1;
        list2[i] = (rand() % 100) + 1;
    }
    
    //Start matrix multiplication
    long result = 0;
    clock_t begin = clock();
    for(int i = 0; i < amt; i++){
        result += list1[i] * list2[i];
    }
    clock_t end = clock();
    
    double time_spent = (double)(end - begin) / CLOCKS_PER_SEC;
    printf("Execution time: %f\n Result is %ld\n", time_spent, result);

    free(list1); free(list2);
    return 0;
}

• Resultat: ca. 0.0065 Sekunden → ca. 4-fach schneller als numpy

numpy - Arrays

• Arbeitet mit (mehrdimensionalen) Arrays (numpy.ndarray)
• Objekt, das numerische Daten eines gemeinsamen Types (dtype) sammelt → unterscheidet sich dadurch von Listen
• Klasse bietet verschiedene Attribute und Methoden an

Beispiel

# Zweidimensionales Array
a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])

# Form des Arrays
a.shape
#> (3,4)

# Typ der Zahlen im Array
a.dtype
#> dtype('int64')

# Zugriff auf erste Zeile
print(a[0])
#> array([1 2 3 4])

# Zugriff auf zweites Element der ersten Zeile
print(a[0][1])
#> 2

numpy - Erstellen von Arrays

• Können direkt aus Python list-Objekten erstellt werden
• Weitere standardisierte Methoden zur Erstellung von Arrays als Funktionen in numpy enthalten

Beispiel

np.zeros(2)
#> array([0., 0.])

np.arange(4)
#> array([0, 1, 2, 3]

np.linspace(0, 10, num=5)
#> array([ 0., 2.5, 5., 7.5, 10.])

np.eye(3)
#>array([[1., 0., 0.],
#>       [0., 1., 0.],
#>       [0., 0., 1.]])

np.logspace(1, 3, num=5)
#> array([10., 31.6227766, 100., 316.22776602, 1000.])

np.empty([2, 2]) # uninitialisierte Werte --> wie in C(++)
#> array([[ -9.74499359e+001,   6.69583040e-309],
#>        [  2.13182611e-314,   3.06959433e-309]])

numpy - Slicing

• das Auswählen von Teilbereichen (Slices) funktioniert analog zu Listen
  
• Filtern ist ebenfalls durch die Eingabe von Filter-Kriteria in die eckigen Klammern möglich
• Dabei beziehen sich die Zahlen auf die Werte im Array und nicht auf die Indexpositionen

Beispiel - Filtern

a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])

c = a[(a > 2) & (a < 11)]
print(c)
#> [ 3  4  5  6  7  8  9 10]

Bildquelle

numpy - Nützliche Funktionen/Methoden

• Viele Funktionen sind direkt als Methoden der numpy.ndarray-Klasse verfügbar
• Andere als Funktionen des numpy-Pakets
• Teils sind beide Varianten verfügbar → Methode operiert direkt auf dem Array, Funktion erstellt neues Array als Kopie

Weitere nützliche Methoden

data = np.array([1, 2, -3, 10, 15, -20])

data.max()
#> 15.0
data.min()
#> -20.0
data.sum()
#> 5.0
data.mean()
#> 0.8333333333333334

Weitere nützliche Funktionen

np.argmax(data)
#> 4
np.resize(data, (2, 3))
#>array([[  1,   2,  -3],
#>       [ 10,  15, -20]])

numpy - math. Operationen

• Die meisten Operationen der linearen Algebra sind für numpy Arrays implementiert
  • Multiplikation mit einem Skalar: scalar * matrix
  • Elementweise Addition zweier gleich dimensionaler Matritzen matrix + matrix
  • Elementweises Anwenden von Funktionen np.square(...)

Arbeiten mit Formeln

Bildquelle

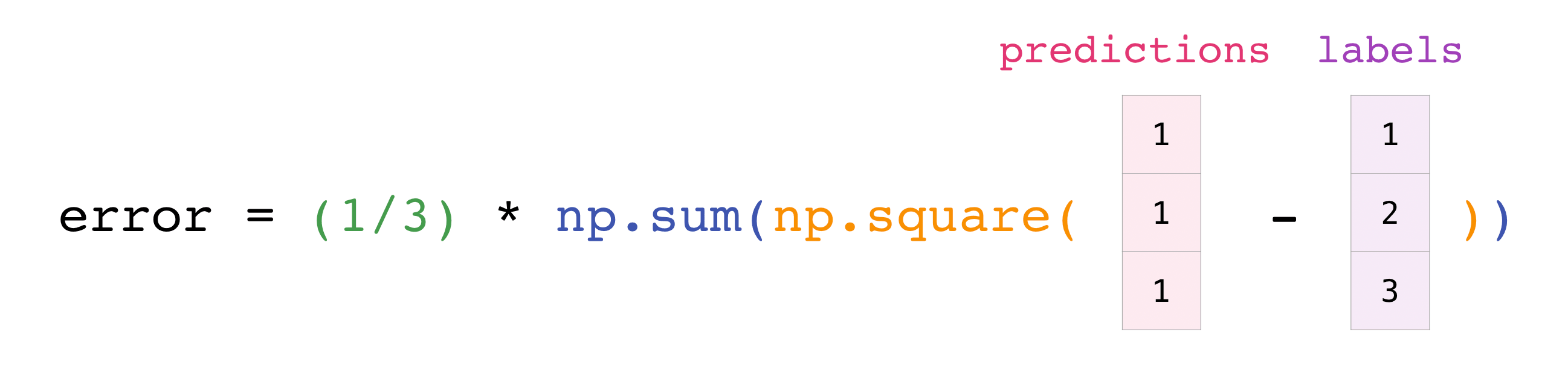
numpy - Broadcasting

• numpy ermöglicht Operationen auf Arrays unterschiedlicher Form
• Arrays werden automatisch erweitert, um die Operation durchzuführen

Beispiel

a = np.array([1, 2, 3])
b = 2
print(a * b)
#> array([2, 4, 6])

• Funktioniert auch in der Anwendung auf Funktionen → in f(x) wird der Skalar b "ausgedehnt" auf die Größe von a

Beispiel

def f(a):
  b = 1
  return a + b

arr = np.array([1, 2, 3, 4, 5])
print(f(arr))

Aufgabe

• Wir wollen nun ein Beispiel aus der Mechatronik mit numpy lösen
  • Die Übertragungsfunktion eines RC-Tiefpassfilters soll bestimmt werden
  • Der Frequenzgang soll mit numpy berechnet werden
  • Der Frequenzgang soll geplottet werden → muss den Anforderungen an einen wissenschaftlichen Plot entsprechen
  • Fehlerfortpflanzung für Bauteiltoleranzen (R & C) soll berechnet werden

Start - numpy_example_filters_inclass_start.ipynb

• Auf dieses Notebook soll aufgebaut werden

Vollständige Musterlösung - numpy_example_filters.ipynb

• Klasse für RC-Tiefpassfilter
• Berechnung des Frequenzgangs
• etc.

Motivation - Wissenschaftliche Plots

• Wir wollen in der Lage sein Daten zu visualiseren
• Dabei wollen wir uns an wissenschaftlichen Standards orientieren → z.B.: für Laborberichte, BA-Arbeiten, etc.
• Hier gibt es einige Regeln, die es zu beachten gilt → viel davon schon automatisch mit matplotlib umsetzbar

Leitfaden: Zitieren und Abbildungen

• Achsen mit Einheiten beschriften ()
• Transparenter oder weißer Hintergrund
• Unterschiedliche Linien auch in schwarz-weiß Kopie unterscheidbar (z.B. durch gestrichelte Linien)
• Vektorgrafik (nicht verpixelt)

Matplotlib - Erster Plot

• matplotlib Plots sind aus "Bausteinen" (siehe rechts) aufgebaut

Beispiel scatter.py

import numpy as np
import matplotlib.pyplot as plt

# generate data to be plotted
x = np.arange(0, 10, 0.1)
y = np.random.rand(100)

# create figure and axis 
# to plot on
fig, ax = plt.subplots()

ax.plot(
  x, #data to plot
  y, #data to plot
  marker='o', #opt. marker style
  linestyle='None' #opt. linestyle
)
plt.show() #actually show it

Bild: matplotlib.org

Matplotlib - Cheat Sheets

• Matplotlib Cheatsheets bzw. Examples/Cheat Sheets

Matplotlib - Styling

• matplotlib bietet viele Möglichkeiten zur Anpassung der Plots

  ax.plot(
      x, y,
      color="g",
      marker="o",
      markersize=12,
      markevery=25,
      markerfacecolor="b",
      markeredgecolor="r",
      linestyle="--",
      linewidth=2,
      label="Datenpunkte"
  )
  

• color: Gibt Farbe an
• marker & markersize: Geben Form & Größe der Marker an
• markevery: Gibt an, wie oft ein Marker gezeichnet wird
• markerfacecolor & markeredgecolor: Farbe des Markers
• linestyle & linewidth: Geben Stil & Breite der Linie an
• label: Legendeneintrag für dieses Element

Matplotlib - Styling

• Beispiel von oben

Beispiel - styling.py

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0.1, 10*np.pi, 1e3)
y = np.sin(x)                        

 #create figure and axis
fig, ax = plt.subplots()
ax.plot(
    x, y,
    color="g",
    marker="o",
    markersize=12,
    markevery=25,
    markerfacecolor="b",
    markeredgecolor="r",
    linestyle="--",
    linewidth=2,
    label="Datenpunkte"
)
plt.tight_layout()
plt.show()
#plt.savefig("plot.svg")

Matplotlib - Farbdarstellung

• Farben können in verschiedenen Formaten angegeben werden
• Eingebaute (Grund-)farben über einzelne Buchstaben verwendbar:
  • color = "b": blau
  • color = "g": grün
  • color = "k": schwarz
  • color = "mediumseagreen": → Liste aller Farben
• Grautöne als String im Bereich von 0-1 → color = "0.75"
• Allgemeine Farben als Hex-Code oder RGB-Tupel im Bereich [0, 1]
  • color = "#eeefff"
  • color = [0.1, 0.3, 0.9]

Matplotlib - Farbdarstellung

Beispiel: MCI-Blau

• Gewöhnliches RGB-Tupel wie in z.B. GIMP oder Photoshop → color = [28, 69, 113] → sind mit 8-Bit Farbtiefe kodiert
• Übliche RGB-Farbwerte umrechnen → color = [28/255, 69/255, 113/255]
• Angabe für matplotlib: color = [0.11, 0.27, 0.44]

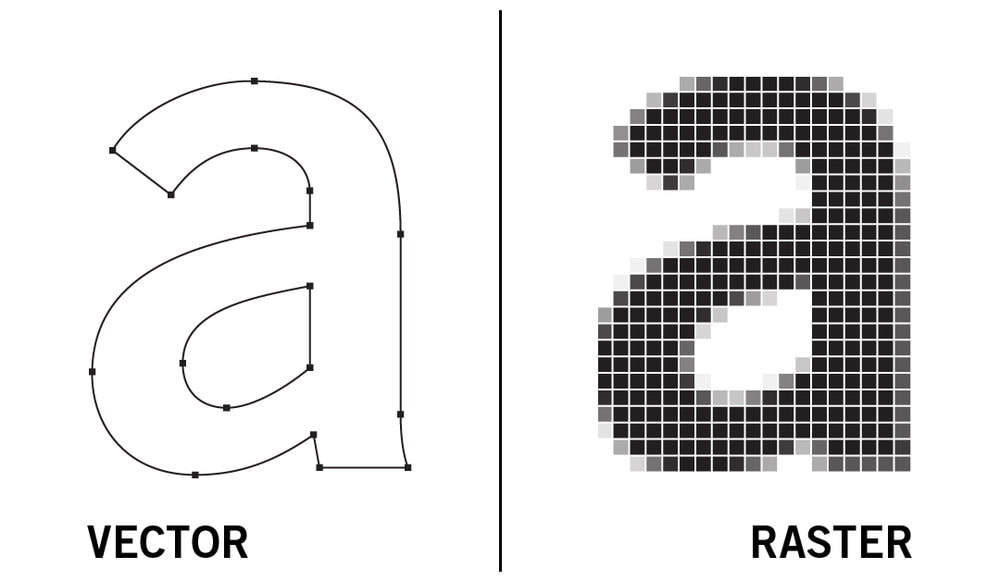
Matplotlib - Bildformate

Rastergrafiken

• Bild wird über Raster von einzelnen Pixeln dargestellt → beim Vergrößern muss interpoliert werden → sieht unprofessionell aus
• Übliche Rasterformate: *.bmp, *.png, *.jpg, *.gif, *.tiff, etc.

Vektorgrafiken

• Speichern Bilder auf der Grundlage von Regeln (normalerweise in einer Auszeichnungssprache) → Linien, Polygone, etc. werden definiert → kann beliebig vergrößert werden
• Übliche Vektorformate: *.pdf, *.svg, *.eps, etc.

  # Beispiel für das Speichern als Vektorgrafik
  plt.savefig("test.pdf")
  

Alternativen zu Matplotlib

• In Python gibt es drei große Module, die häufig zur Erstellung von Diagrammen verwendet werden:

Module zur Visualisierung

• matplotlib:
  • wirkt etwas altmodisch, komplizierte Befehle, wenig aufgeräumt
• seaborn:
  • baut auf matplotlib auf, man erhält schneller schöne Graphen, basierend auf "tidy data" Prinzipien
• plotly:
  • modernes Design, ermöglicht interaktive Grafiken

Aufgabe

• Um das Verständnis für matplotlib weiter zu vertiefen kann das hier verlinkte Notebook bearbeitet werden.
• Notebook: matplotlib - Daten visuell darstellen

Hausübung

• Erweitern Sie die Datenverarbeitungs-Pipeline aus der letzten Hausübung um die Möglichkeit Polynome auf die Daten zu fitten
• Nutzen Sie hierzu NICHT die direkten Funktionen von numpy sondern implementieren Sie die Berechnung selbst → dies ist durch aufstellen & lösen eines linearen Gleichungssystems möglich
• Plotten Sie anschließend die Datenpunkte und das gefittete Polynom